Dicke Ringe bewegen sich mehr, so dass man leichter an sie erinnert wird.
Sind Piercingringe nicht nur Schmuck für einen, sondern auch zum spielen da, sollten sie dick (![]() 2 mm) sein. Wenn man sie belastet, wachsen sie nicht so leicht heraus (man denke an einen Käseschneider, bei dem ein dünner Draht zum schneiden verwendet wird) und vor allem:
2 mm) sein. Wenn man sie belastet, wachsen sie nicht so leicht heraus (man denke an einen Käseschneider, bei dem ein dünner Draht zum schneiden verwendet wird) und vor allem:
Dicke Ringe bewegen sich mehr, so dass man leichter an sie erinnert wird.
Aber warum ist das so?
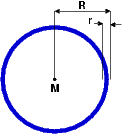
Sei ![]() der Radius des Ringes und
der Radius des Ringes und ![]() der Radius des Ringmaterials (wir sprechen hier von einem Torus).
der Radius des Ringmaterials (wir sprechen hier von einem Torus).
Dass man einen solchen Ring beim Bewegen spürt, liegt natürlich daran, dass er sich wie ein angestoßenes Pendel verhält, also eine gedämpfte, anharmonische Oszillation vollführt. Da bei unserem idealisierten Piercing der Schwerpunkt exakt in der Mitte liegt, sollte es mit der Frequenz
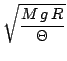 |
|||
schwingen, wobei
![]() die Erdbeschleunigung und
die Erdbeschleunigung und ![]() die Masse des Ringes ist.
die Masse des Ringes ist.
Das Trägheitsmoment bzgl. Drehungen um den Schwerpunkt lässt sich mit
![]() recht leicht bestimmen.
recht leicht bestimmen.
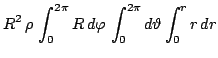 |
|||
Die Drehung des Schwerpunktes um den oberen Rand des Ringes ist ein wenig aufwändiger zu erfassen. Die Punkte des Torus kann man wie folgt parametrisieren:
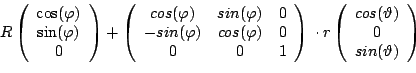 |
|||
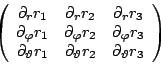 |
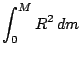 |
|||
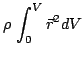 |
|||
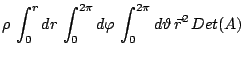 |
|||
Die Reibung des Ringes an der Haut hängt von der Kontaktfläche ab, welche natürlich ein Bruchteil ![]() der gesamten Oberfläche ist.
der gesamten Oberfläche ist.
Die Rückstellkraft bei einer Auslenkung ![]() des Ringes aus seiner Ruhelage ist
des Ringes aus seiner Ruhelage ist
Man erkennt, dass der Antrieb der Schwingung bei einer Vergrößerung von ![]()
![]() -mal stärker als die Reibung wächst.
-mal stärker als die Reibung wächst.
Hinzu kommt, dass dickere Ringe meistens auch einen größeren Radius ![]() haben. Während
haben. Während
![]() ist, wächst
ist, wächst
![]() !
!
Das erklärt, warum man dicke Piercingringe stärker spürt.
8-)